행렬
- 행렬(Matrix): A = [aᵢⱼ]
- n, m이 양의 정수일 때 n행, m열로 나열된 실수의 2차원 배열
- 가로줄을 행(Row), 세로줄을 열(Column)
- 행 크기와 열 크기 → 행렬의 크기
- aᵢⱼ: 행렬 A의 i행, j열 원소
행렬의 연산
행렬의 덧셈과 뺄셈
- 두 행렬 A, B에서 같은 자리에 있는 원소들끼리 더하거나 빼는 연산
- 두 행렬의 크기가 같아야만 연산 가능(두 행렬의 행과 열의 크기가 각각 같음)
스칼라곱
- kA = Ak = [kaᵢⱼ]
- 행렬 A에 실수 k를 곱하는 연산
- 행렬의 각 원소마다 그 실수 값을 곱함
행렬의 곱셈
- n × m 행렬 A와 r × s 행렬 B가 있고 m = r 일 때, n × s 행렬 A·B = [cᵢⱼ]

- 행렬 A의 i번째 행과 행렬 B의 j번째 열이 서로 대응하여 연산되기 때문에 행렬 A의 열 크기와 행렬 B의 행 크기가 같아야 함
- 행렬 A의 크기가 n × m이고 행렬 B의 크기가 m × s 일 때 곱 AB의 결과로 나오는 행렬의 크기는 n × s
행렬의 종류
- 영행렬(Zero Matrix, O): n × m 행렬 A = [aᵢⱼ] 가 있을 때, 모든 i, j에 대하여 aᵢⱼ = 0 인 행렬
- n차 정사각행렬(n-Square Matrix): n × m 행렬 A = [aᵢⱼ] 가 있을 때, m = n 인 행렬
- 대각행렬(Diagonal Matrix): n차 정사각행렬에서 대각원소(a₁₁, a₂₂, ... , aₙₙ) 이외의 모든 원소가 0인 행렬
- 단위행렬(항등행렬, Unit Matrix, Identity Matrix, I): 대각행렬에서 대각원소가 모두 1인 행렬
- 행렬의 곱셈에서 AI = IA = A이기 때문에 항등행렬이라고도함(행렬의 곱셈의 항등원)
- 단위행렬과의 곱셈 연산은 항상 교환법칙이 성립함
- 전치행렬(Transpose Matrix, Aᵀ): n × m 행렬 A = [aᵢⱼ] 가 있을 때, 행과 열을 바꾼 m × n 인 행렬
- 대칭행렬(Symmetric Matrix): n차 정사각행렬 A = [aᵢⱼ] 가 있을 때, Aᵀ = A 인 행렬
부울행렬
- 행렬의 모든 원소가 부울값(0과 1)으로만 구성된 행렬
- 원소 간의 관계를 표현하거나 관계를 합성하는 데에 유용하게 사용되는 행렬
- 0과 1로만 표현되기 때문에 일반 행렬과 다른 연산 방식을 사용
부울행렬 연산자
- A = [aᵢⱼ], B = [bᵢⱼ]
- 합: A ∨ B = [aᵢⱼ ∨ bᵢⱼ]
- 곱: A ∧ B = [aᵢⱼ ∧ bᵢⱼ]
- 부울곱: A ⊙ B, n × m 부울행렬 A와 m × s 부울행렬 B가 있을 때, n × s 부울행렬 A ⊙ B = [cᵢⱼ]
- A ⊙ B = [cᵢⱼ] = (aᵢ₁∧b₁ⱼ) ∨ (aᵢ₂∧b₂ⱼ) ∨ ... ∨ (aᵢₘ∧bₘⱼ)
부울행렬의 합
- 논리합(∨) 연산과 같은 방식으로 연산
- 행렬 A의 원소인 aᵢⱼ와 행렬 B의 원소인 bᵢⱼ 중 하나라도 1이면 합 연산의 결과는 1이 됨
부울행렬의 교차
- 논리곱(∧) 연산과 같은 방식으로 연산
- 행렬 A의 원소인 aᵢⱼ와 행렬 B의 원소인 bᵢⱼ 모두 1인 경우에만 교차 연산의 결과가 1이 됨
부울행렬의 부울곱
- 행렬의 곱셈 방식과 논리합 & 논리곱의 연산을 적용하여 수행
부울행렬 연산의 특징
| A ∨ A = A | A ∧ A = A | |
| A ∨ B = B ∨ A | A ∧ B = B ∧ A | |
| (A ∨ B) ∨ C = A ∨ (B ∨ C) | (A ∧ B) ∧ C = A ∧ (B ∧ C) | A ⊙ (B ⊙ C) = (A ⊙ B) ⊙ C |
| A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C) | A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) |
행렬식
- Determinant, |A|, det(A)
- n차 정사각행렬에 대응하는 함수
- 2차 정사각행렬 A의 행렬식: det(A) = a₁₁a₂₂ - a₁₂a₂₁
- 3차 정사각행렬 B의 행렬식: det(B) = (b₁₁b₂₂b₃₃ + b₁₂b₂₃b₃₁ + b₁₃b₃₂b₂₁) - (b₁₃b₂₂b₃₁ + b₂₃b₃₂b₁₁ + b₃₃b₂₁b₁₂)

소행렬
- Minor Matrix, Mᵢⱼ
- n차 정사각행렬에서 i번째 행과 j번째 열을 제거해서 얻은 (n - 1) × (n - 1) 행렬
- 소행렬식(det(Mᵢⱼ)): n차 정사각행렬의 소행렬 Mᵢⱼ에 대한 행렬식
여인수행렬
- Cofactor Matrix, [Aᵢⱼ]
- n차 정사각행렬 A = [aᵢⱼ]에서 원소 aᵢⱼ에 관련된 계수와 그 계수들의 행렬
- Aᵢⱼ = (-1)ⁱ⁺ʲ·det(mᵢⱼ)
- 여인수는 행렬식을 구하는 식에서 행렬 A의 원소 aᵢⱼ의 계수가 되는 수로 소행렬식에 의해 결정됨
- 여인수행렬 내에서의 위치에 따라 부호가 정해짐
여인수를 이용한 행렬식
- 행렬식을 구해야 하는 n차 정사각행렬에서 행이나 열 중에서 하나를 선택하여 해당하는 원소의 여인수와 곱한 후 그 결과를 더하여 구하는 방식
- i행을 선택한 경우: det(A) = aᵢ₁Aᵢ₁ + aᵢ₂Aᵢ₂ + ... + aᵢₙAᵢₙ
- j열을 선택한 경우: det(A) = a₁ⱼA₁ⱼ + a₂ⱼA₂ⱼ + ... + aₙⱼAₙⱼ
역행렬
- Inverse Matrix, A⁻¹
- 정사각행렬 A에 대해 AB = BA = I를 만족하게 하는 행렬 B
- AA⁻¹ = A⁻¹A = I
- A = (a)의 경우 det(A) = a ≠ 0 → A⁻¹ = 1/a
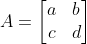

행렬식을 이용한 역행렬
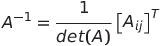
- 단, det(A) ≠ 0
수반행렬
- Adjoint Matrix, [Aᵢⱼ]ᵀ
- 여인수행렬 [Aᵢⱼ]에 대한 전치행렬
가역행렬
- Invertible Matrix
- det(A) ≠ 0인 행렬, 역행렬이 존재하는 행렬
특이행렬
- Singular Matrix
- det(A) = 0인 행렬, 역행렬이 존재하지 않는 행렬
1차방정식
- Linear Equation, 선형방정식
- a₁, a₂, ..., aₙ, b가 실수일 때, a₁x₁ + a₂x₂ + ... + aₙxₙ = b와 같이 표현되는 식
- a₁, a₂, ..., aₙ: 계수
- b: 상수
- x₁, x₂, ..., xₙ: 미지수
- 1차방정식은 미지수끼리의 곱이나 제곱근이 포함되지 않고, 모든 미지수가 1차로 표현
- 해: 1차방정식에 포함된 n개의 미지수에 대해 x₁ = s₁, x₂ = s₂, ... , xₙ = sₙ을 만족하는 s₁, s₂, ... , sₙ
연립1차방정식
- System of Linear Equation
- 1차방정식 m개로 구성된 방정식

- 행렬들을 AX = B의 형태로 연산하면 연립1차방정식과 같은 형태
- 행렬 A를 계수행렬 (m × n), 행렬 X를 미지수행렬 (n × 1), 행렬 B를 상수행렬 (m × 1)이라고 함

첨가행렬
- Augmented Matrix
- 연립1차방정식의 계수행렬 A와 상수행렬 B를 다음과 같은 형태로 구성한 행렬

가우스 행렬
- Gauss Matrix
- 계수행렬의 대각원소들을 모두 1로 만들면서, 대각원소를 기준으로 아래쪽 원소들은 모두 0이 되도록 하고, 위쪽 원소들은 계수들로 남겨놓은 형태의 첨가행렬

가우스 행렬을 만들기 위한 연산
- 한 행에 0이 아닌 스칼라곱을 함
- 스칼라곱을 한 행과 다른 행을 더해 원소를 0으로 만듦
가우스 조르단 소거법
- 가우스 소거법에서 조금 더 연산을 수행하여 첨가행렬 중 계수 부분을 모두 단위행렬의 형태로 만듦
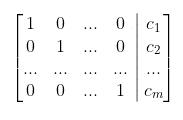
- 가역행렬인 경우, 가우스 조르단 소거법을 이용해 역행렬을 구할 수 있음
- 첨가행렬의 왼쪽에는 가역행렬, 오른쪽 부분에 단위행렬을 놓고 첨가행렬의 왼쪽 부분이 단위행렬의 형태가 될 때까지 가우스 조르단 소거법을 수행하면 오른쪽 부분은 역행렬이 됨

