트리
- 루트라는 특별한 노드를 갖고 그래프를 구성하는 꼭짓점 u, v 간에 u에서 v로 가는 단순경로가 존재하는 비순환의 연결 그래프
- 나무의 가지가 뿌리에서 뻗어나가듯이 트리는 루트를 중심으로 하나 이상의 꼭짓점(노드)들이 비선형이면서 비순환적인 경로로 연결되어 있는 형태
- 노드: 트리인 그래프를 구성하는 꼭짓점
- 루트: 트리인 그래프의 가장 높은 곳에 위치하는 시작 노드
- 서브 트리: 트리인 그래프의 임의의 한 노드를 루트로 하는 트리
- 차수: 트리인 그래프의 임의의 한 노드에 포함된 자식 노드의 개수
- 레벨: 트리인 그래프의 루트 노드를 레벨 0으로 시작하여 자식 노드로 한 단계씩 내려갈 때마다 하나씩 증가하는 단계
- 높이/깊이: 트리인 그래프의 최대 레벨
- 포레스트: 트리인 그래프의 루트 노드와 가지를 제거하여 얻는 서브 트리들
- 트리에서 노드의 개수를 v, 모서리의 개수를 e라고 하면 e = v - 1
트리의 노드
- 부모 노드: 임의의 노드의 한 단계 상위 노드
- 자식 노드: 임의의 노드의 한 단계 하위 노드
- 형제 노드: 임의의 노드와 부모가 같은 노드
- 리프 노드: Leaf Node, 노드들 중 자식 노드가 없는 노드
- 중간 노드: 노드들 중 루트 노드나 리프 노드가 아닌 노드
- 조상 노드: 루트 노드에서 임의의 한 노드에 이르는 경로에 포함된 모든 노드들
- 자손 노드: 임의의 한 노드에서 리프 노드에 이르는 경로에 포함된 모든 노드들
이진 트리
- 트리인 그래프의 차수가 최대 2인 트리
- 트리의 최대 차수가 n이라면 n항 트리(n-ary tree)
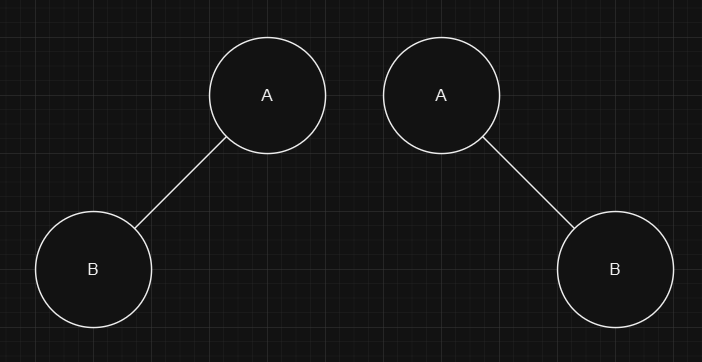
- 위의 두 트리는 노드의 수, 노드의 이름, 모서리의 수, 트리의 높이가 같지만 자식 노드의 위치가 다르기 때문에 전혀 다른 트리로 취급
- 완전 이진 트리: Complete Binary Tree, 높이가 h일 때 레벨 0부터 h-1까지의 모든 부모 노드의 차수가 2차이고, 레벨 h는 왼쪽부터 노드가 채워져 있는 트리
- 포화 이진 트리: Full Binary Tree, 높이가 h일 때 레벨 0부터 h-1까지의 모든 노드의 차수가 2차인 트리
- 편향 이진 트리: Skewed Binary Tree, 왼쪽이나 오른쪽 서브 트리만 가지는 트리
이진 트리의 노드
- 이진 트리는 부모 노드가 가질 수 있는 자식 노드의 수가 2개 이하이기 때문에 노드의 수 예측이 가능
- 레벨 k에서 가질 수 있는 최대 노드 수: 2ᵏ개
- 높이가 m인 이진 트리가 가질 수 있는 최대 노드 수: 2ᵐ⁺¹ - 1개
- 높이가 m인 이진 트리가 가질 수 있는 최소 노드 수: m+1개
이진 트리의 구현
- 높이가 h인 완전 이진 트리는 각 노드 번호로 1차원 배열을 구현 가능
- 루트 노드의 인덱스는 1
- 형제 노드 중 왼쪽 노드의 인덱스 순서가 오른쪽 노드보다 빠름
노드의 인덱스
- 부모 노드의 인덱스가 n일 때, 왼쪽 자식 노드는 2n, 오른쪽 자식 노드는 2n+1
- 편향 이진 트리의 경우 각 노드의 인덱스에 해당하는 배열의 인덱스에 입력하기 때문에 배열에 빈자리가 발생
- 메모리 공간의 낭비, 이진 트리를 배열로 표현하는 것이 비효율적인 이유
- 배열에서 이진 트리 노드의 삽입과 삭제는 인덱스 i 이후에 위치하고 있는 노드들의 수만큼의 연산과 이동 시간이 필요하기 때문에 비효율적
연결리스트로 구현한 이진 트리
- 부모 노드와 자식 노드를 포인터로 연결하므로 연속된 메모리 영역이 아니더라도 부모와 자식 노드를 인결할 수 있음
- 연결리스트 노드 구성: 왼쪽 자식 노드의 주소 - 데이터 - 오른쪽 자식 노드의 주소
- 연결리스트의 양쪽 노드는 자식 노드의 주소를 가지게 되는데 리프 노드의 경우는 자식 노드를 갖지 않기 때문에 자식 주소가 들어가는 영역에 null이 입력
순회
- 모든 노드의 데이터를 처리할 수 있도록 한 번씩 방문하는 방법
- 항상 루트 노드에서 시작
- 노드의 데이터를 읽기 전에 노드가 존재하는지 먼저 탐색
- 형제 노드 중 왼쪽 노드를 항상 먼저 탐색
전위순회
- Preorder Traversal
- 부모 노드 - 왼쪽 자식 노드 - 오른쪽 자식 노드 순으로 탐색하는 순회 방식
중위순회
- Inorder Traversal
- 왼쪽 자식 노드 - 부모 노드 - 오른쪽 자식 노드 순으로 탐색하는 순회 방식
후위순회
- Postorder Traversal
- 왼쪽 자식 노드 - 오른쪽 자식 노드 - 부모 노드 순으로 탐색하는 순회 방식
순회를 이용한 수식의 표현
- 수식 (a+b) × (c-d) 라는 연산을 수행
- 변수 a, b에 값을 입력
- (a+b) 계산
- 변수 c, d에 값을 입력
- (c-d) 계산
- (a+b) × (c-d)

